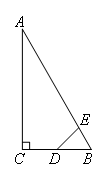
如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以
1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒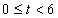（），连接DE，
当△BDE是直角三角形时，t的值为(    )

1．解题要点
①研究基本图形，分析运动状态，分段定范围．
△ABC是含30°角的直角三角形，BC=2，，AB=4，BD=1，

∴，
结合题目中的条件，，
∴．
②分析特征有序思考，设计方案．
分析定点、动点：△BDE中，B，D是定点，E是动点，且∠DBE=60°不变；
确定分类标准：分别以D，E为直角顶点分类讨论．
③根据方案作出图形，有序操作．
当点D，E为直角顶点时，画出符合题意的图形，利用特殊角度或相似求解．
④结果检验、总结．
作图验证，根据图形对结果进行判断；分析数据，对结果进行验证取舍．
2．解题过程
在Rt△ABC中，∠ACB=90°，BC=2，
∴AB=4．
∵D是BC的中点，
∴BD=1．
由题意，∠DBE=60°，若△BDE为直角三角形，则需分别以点D，E为直角顶点讨论：
①当∠EDB=90°时，如图，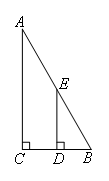

点E从A到B运动时，
在Rt△EDB中，BD=1，∠B=60°，
∴EB=2，
∴AE=AB-EB=2．
∵点E运动的速度是1cm/s，
∴t=2．
点E从B到A运动时，
t=4+2=6（舍）．
②当∠DEB=90°时，如图，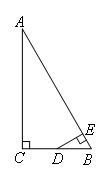

点E从A到B运动时，
在Rt△EDB中，BD=1，∠B=60°，
∴，
∴．
∵点E运动的速度是1cm/s，
∴t=3.5．
点E从B到A运动时，
t=4+0.5=4.5．
∴当△BDE是直角三角形时，t的值为2或3.5或4.5．
故选D．

略