如图,从一个直径为2的圆形铁皮中剪下一个圆周角为60°的扇形ABC,若剪下来的扇形恰能围成一个圆锥,则该圆锥的底面圆半径为( )

- A.
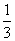
- B.
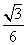
- C.
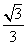
- D.
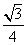
答案
正确答案:B
如图,连接OA,OB,OC,过点O作OD⊥AB于点D.

则AB=2AD,
易证△ABO≌△ACO,
∴∠BAO=∠CAO=30°.
在Rt△AOD中,OA=1,∠DAO=30°,
∴![]() ,
,
∴![]() ,
,
 .
.
设圆锥的底面圆半径为r,则![]() ,
,
∴![]() ,即该圆锥的底面圆半径为
,即该圆锥的底面圆半径为![]() .
.
故选B.
略








