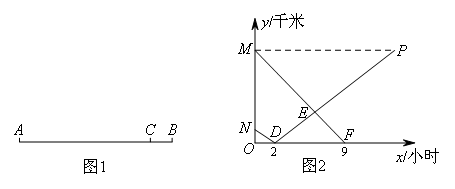
A,B两地相距630千米,客车、货车分别从A,B两地同时出发,匀速相向行驶(客车的终点站是C站,货车的终点站是A站),客车需9小时到达C站,货车2小时可到达图中C站(如图1所示),货车的速度是客车的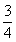 ,客车、货车到C站的距离y与行驶时间x(小时)之间的函数关系如图2所示.则两车同时出发后,相距360千米的时刻是( )
,客车、货车到C站的距离y与行驶时间x(小时)之间的函数关系如图2所示.则两车同时出发后,相距360千米的时刻是( )
- A.6
- B.
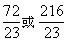
- C.
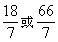
- D.
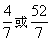
答案
正确答案:C
知识点:一次函数应用题
根据图象可得,货车从B站到C站需要2小时,客车从A站到C站需要9小时,设客车的速度为x千米/小时,则货车的速度为![]() 千米/小时,则:
千米/小时,则:![]() ,
,
解得:x=60,即:客车的速度为60千米/小时,则货车的速度为45千米/小时,
∴AC两站间距离为540千米,BC两站间距离为90千米,
在图象上即:M(0,540),N(0,90),
∴ND段表达式为:y=-45x+90(0≤x≤2),
MF段表达式为:y=-60x+540(0≤x≤9),
∵整个过程中货车的速度不变,
∴DP段的斜率为45,
结合D点坐标可得DP段表达式为:y=45x-90(2<x≤14),
∵当x=2时,两车之间的距离为420千米,
∴两车相距360千米的时刻应该在2小时之后,
两车相距360千米,在图象上表现即为:yMF-yDP=360或yDP-yMF=360,
即:-60x+540-(45x-90)=360或45x-90-(-60x+540)=360,
解得:![]() .
.
故选C.
略








