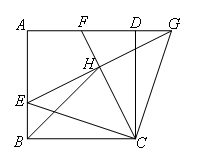
如图,在边长为 的正方形ABCD中,E是AB边上的一点,G是AD延长线上一点,
的正方形ABCD中,E是AB边上的一点,G是AD延长线上一点,
BE=DG,连接EG,CF⊥EG于点H,交AD于点F,连接CE,BH.若BH=8,则FG=( )
- A.

- B.
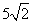
- C.

- D.
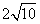
答案
正确答案:B
知识点:相似三角形的判定和性质 旋转结构
如图,过点H作MN⊥AD,交AD于点N,交BC于点M,延长BC至点P,使CP=BE,连接HP,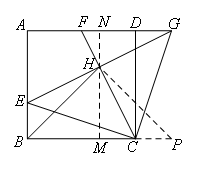
∵四边形ABCD是正方形,
∴BC=CD,∠EBC=∠CDG=∠BCD=90°.
∵BE=DG,
∴Rt△CBE≌Rt△CDG,
∴CE=CG,∠ECB=∠GCD,∠BEC=∠DGC,
∴∠ECG=∠BCD=90°.
∵CF⊥EG,
∴CH=HE,∠CEH=∠HCG=45°.
∵∠DGC=∠GCP,
∴∠HEC+∠BEC=∠HCG+∠GCP,即∠HEB=∠HCP.
∵BE=CP,
∴△HEB≌△HCP(SAS),
∴HB=HP,∠EHB=∠CHP.
∵∠EHC=90°,
∴∠BHP=90°,
∴△BHP为等腰直角三角形.
∵BH=8,MN⊥AD,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
易得Rt△HNF∽Rt△HMC∽Rt△GNH,
∴![]()
∴![]() ,
,
∴![]() .
.
故选B.
略








