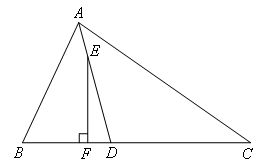
已知：如图，在△ABC中，AD是∠BAC的平分线，E为AD上一点，且EF⊥BC于点F．
若∠C=35°，∠DEF=15°，则∠B的度数为(    )

要求∠B的度数，可以放到△ABC中，利用三角形的内角和等于
180°求解，只要能求出∠BAC的度数即可．
由垂直可以想到直角三角形两锐角互余，已知∠DEF=15°，
利用互余求得∠EDF=75°，然后把∠EDF看成△ACD的一个外角，
通过外角来转角，由∠C=35°，得到∠CAD=40°，
因为AD是∠BAC的平分线，所以∠BAC=2∠CAD=80°，
在△ABC中，利用三角形的内角和等于180°，求得∠B=65°．
故选B．

略