已知:如图,BF∥DG,AD∥EF,∠ACF=70°,∠G=30°.
求∠EFG的度数.
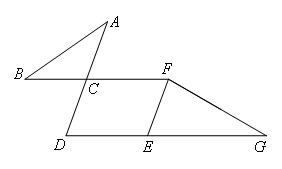
证明:如图,
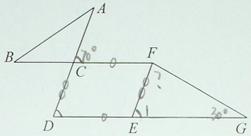
∵BF∥DG(已知)
∴∠ACF= (两直线平行,同位角相等)
∵AD∥EF(已知)
∴∠D= (两直线平行,同位角相等)
∴∠ACF=∠1(等量代换)
∵∠ACF=70°(已知)
∴∠1=70°(等量代换)
在△FEG中,∠1=70°,∠G=30°
∴∠EFG=180°-∠1-∠G
=180°-70°-30°
=80°( )
①∠CFE;②∠D;③∠1;④∠ACF;⑤平角的定义;⑥三角形的内角和等于180°.
以上空缺处依次所填正确的是( )
- A.①③⑤
- B.①④⑥
- C.②③⑥
- D.②④⑤
答案
正确答案:C
要求∠EFG的度数,考虑放在△EFG中利用三角形的内角和等于180°来求解,
已知∠G=30°,只要求出∠1的度数即可,
已知∠ACF=70°,因此利用平行线的性质转移角.
由BF∥DG,利用两直线平行,同位角相等,得∠ACF=∠D(因此第一个空选②).
由AD∥EF,利用两直线平行,同位角相等,得∠D=∠1(因此第二个空选③).
已知∠ACF=70°,利用等量代换,得∠1=70°,在△EFG中,∠1=70°,∠G=30°,利用三角形的内角和等于180°,得∠EFG=80°(因此第三个空选⑥).
故选C.
略









