如图，在梯形ABCD中，AD∥BC，点E在BC上，点F是CD的中点，且AF⊥EF，
若AD=2，BE=AE=5，则BC的长为(    )

如图，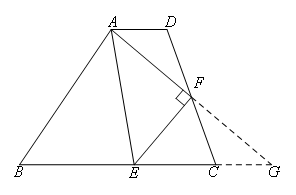

延长AF交BC的延长线于点G，
∵AD∥BC
∴∠DAF=∠CGF
∵点F是CD的中点
∴CF=DF
在△ADF和△GCF中，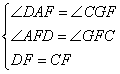

∴△ADF≌△GCF（AAS）
∴AF=GF，CG=AD=2
又∵AF⊥EF
∴AE=GE=5
∴BC=BG-CG=10-2=8
故选C

略