如图，在平面直角坐标系中，抛物线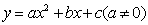的图象经过M(1,0)和N(3,0)两点，且与轴交于D(0,3)，直线l是抛物线的对称轴.
(1)求该抛物线的解析式；
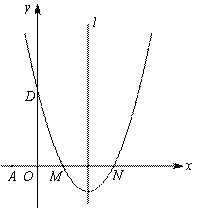
(2)若过点A(-1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6，求此直线的解析式；
(3)在（2）的条件下点P在抛物线的对称轴上，⊙P与直线AB和x轴都相切，求点P的坐标.

（1）∵抛物线y=ax²+bx+c（a≠0）的图象经过M（1，0）和N（3，0）两点，且与y轴交于D（0，3），易求抛物线的解析式为：y=x²﹣4x+3；
（2）设AB所在直线的解析式为：y=kx+b，抛物线的对称轴与x轴的交点为E，则AE=3
当点B在x轴的上方时，
∵抛物线的对称轴和x轴围成的三角形的面积为6
∴BE=4
∴B（2,4）
易求直线AB解析式为：y=x+
当点B在x轴的下方时，同理可求点B的坐标为（2，-4），
∴直线AB的解析式为：y=-x-
（3）过点P作PF⊥AB于点F，设半经PE=PF=r
当点B在x轴的上方时，
1’如图

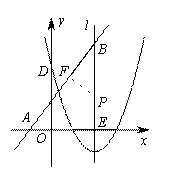
∵∠B＝∠B，∠BEA＝∠BFP
∴△BPF∽BAE
∴，即：
∴
∴点P的坐标为（2，）
2’如图

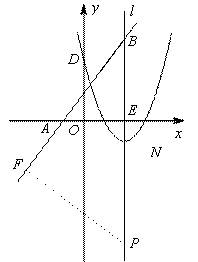
∵∠B＝∠B，∠BEA＝∠BFP＝
∴△BPF∽BAE
∴，即：
∴
∴点P的坐标为（2，-6）
当点B在x轴的下方时，同理可得点P的坐标为（2，）和（2，6）.
综上所述，点P的坐标为（2，）、（2，）、（2，-6）、（2，6）.

略