如图1，正方形ABCD中，在AB，BC边上分别取点M，N，使AM=BN，连接AN，DM交于点O，容易证明∠DON=90°．

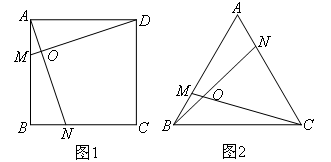
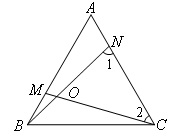
（1）如图2，正三角形ABC中，在AB，AC边上分别取点M，N，使BM=AN，连接BN，CM交于点O，
要证明∠NOC=60°，下列证明思路中不正确的是(    )

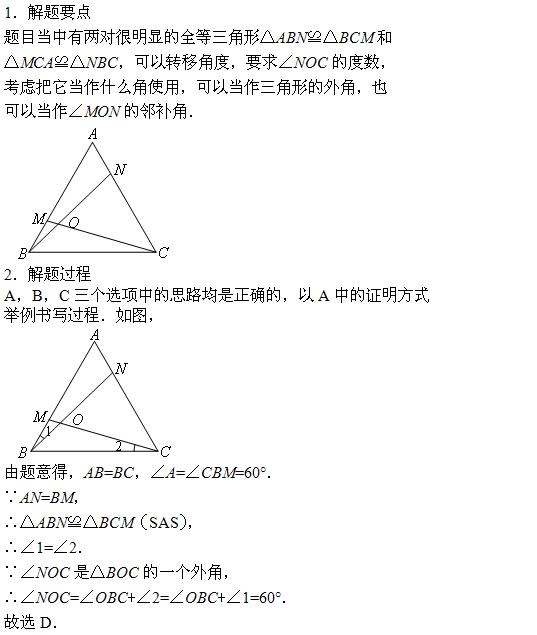
• A.如图，
  
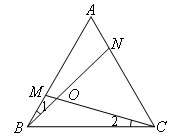
  证明△ABN≌△BCM，得到∠1=∠2，
  ∴∠NOC=∠OBC+∠2=∠OBC+∠1=60°．
• B.如图，
  
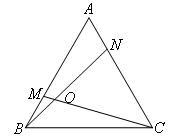
  证明△ABN≌△BCM，得到∠ANB=∠BMC，
  ∴∠ANB+∠AMO=180°，
  ∴∠MON+∠A=180°，
  ∴∠NOC=∠A=60°．
• C.如图，
  
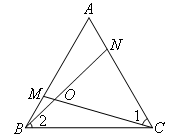
  证明△MCA≌△NBC，得到∠1=∠2，
  ∴∠NOC=∠2+∠OCB=∠1+∠OCB=60°．
• D.如图，
  
  ∵∠NOC+∠1+∠2=180°，
  ∵∠1=80°，∠2=40°，
  ∴∠NOC=60°．

答案

正确答案：D

知识点：中考数学几何中的类比探究  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>