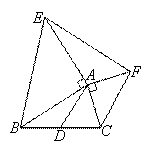
如图，在△ABC中，AD是BC边上的中线，分别以AB边、AC边为直角边各向外作等腰直角三角形，求证：EF=2AD.

答案

延长AD至点G，使DG=AD，连接BG.

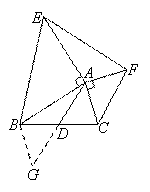
∵AD是BC边上的中线，
∴BD=CD
又∵DG=AD，∠ADC=∠GDB，
∴△ADC≌△GDB（SAS）
∴AC=BG，∠ACB=∠GBD
又∠BAC+∠EAF=180°，∠BAC+∠ACB+∠ABC=180°
∴∠EAF=∠ACB+∠ABC=∠GBD+∠ABC=∠ABG
又AE=AB，AF=AC=BG
∴△ABG≌△EAF（SAS）
∴EF=AG=2AD.

知识点：全等三角形的性质  全等三角形的判定  

这道题目在做辅助线的时候从结论特征出发，看到中线的两倍就想到倍长中线

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>