已知:如图,△ABC和△CDE均为等腰直角三角形,∠ABC=∠CDE=90°,AB=BC,DC=DE,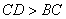 ,点C,B,D在同一直线上,M是AE的中点.
,点C,B,D在同一直线上,M是AE的中点.
求证:MD⊥MB,MD=MB.
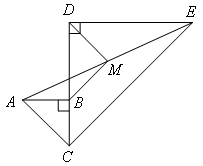
证明:如图,延长BM交DE于点N.
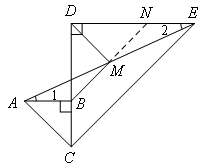
∴∠1=∠2
∵M是AE的中点
∴AM=EM
在△ABM和△ENM中

∴△ABM≌△ENM(ASA)
∴AB=EN,BM=NM
∴DB=DN
∴DM⊥BM,DM平分∠BDN
请你仔细观察下列序号所代表的内容:
①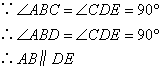 ;②
;②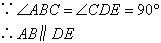 ;③
;③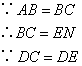 ;
;
④∵DC=DE;⑤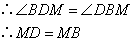 ;⑥
;⑥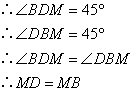 .
.
以上空缺处依次所填最恰当的是( )
- A.①⑤⑥
- B.②④⑤
- C.②③⑤
- D.①③⑥
答案
正确答案:D
知识点:等腰三角形三线合一 全等三角形之倍长中线

略










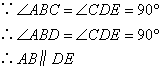 ;②
;②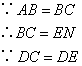 ;
;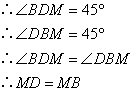 .
.