如图,在正方形ABCD中,点E在CB延长线上,点F在DC延长线上, EAF=45°,则下列结论正确的是( )
EAF=45°,则下列结论正确的是( )
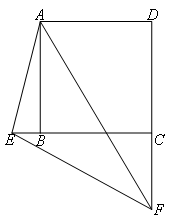
- A.EF=BE+DF
- B.DF=BE+EF
- C.DF=AE+CF
- D.EF=AB+CF
答案
正确答案:B
知识点:三角形全等之截长补短
根据选项特征,这是几条线段间的数量关系,
考虑用截长补短转化成两条线段的等量关系.
解:如图,在DF上截取DG=BE,连接AG.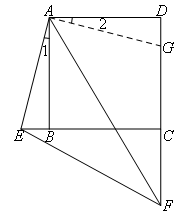
在正方形ABCD中,AD=AB,∠D=∠ABC=∠ABE=90°
在△ADG和△ABE中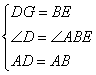
∴△ADG≌△ABE(SAS)
∴AG=AE,∠2=∠1
∵∠2+∠BAG=90°
∴∠1+∠BAG=90°
即∠EAG=90°
∵![]() EAF=45°
EAF=45°
∴![]() EAF=
EAF=![]() GAF=45°
GAF=45°
在△AFE和△AFG中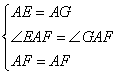
∴△AFE≌△AFG(SAS)
∴EF=GF
∵DF=DG+GF
∴DF=BE+EF
故选B.
略








