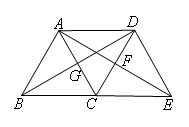
如图，点B，C，E在同一条直线上，△ABC与△CDE都是等边三角形，连接AD，BD，AE，BD交AC于点G，AE交CD于点F．则下列结论不一定成立的是(    )

∵△ABC和△CDE都是等边三角形，
∴BC=AC，CE=CD，∠BCA=∠ECD=60°，
∴∠BCA+∠ACD=∠ECD+∠ACD，
即∠BCD=∠ACE，
∴在△BCD和△ACE中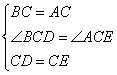
，
∴△BCD≌△ACE（SAS），
故选项A成立；
∴∠DBC=∠CAE，
∵∠BCA=∠ECD=60°，
∴∠ACD=60°，
在△AFC和△BGC中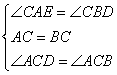
，
∴△AFC≌△BGC（ASA），
故选项B成立；
∵△BCD≌△ACE，
∴∠CDB=∠CEA，
在△DCG和△ECF中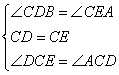
，
∴△DCG≌△ECF（ASA），
故选项C成立．
选项D因为两个等边三角形的大小不确定，所以∠BAD的度数不确定，而∠ACE始终等于120°，故两个三角形不一定全等．
故选D

略