已知:如图,在等边三角形ABC中,∠C=∠ABD=60°,AB=BC=AC,点D,E分别为BC,AC边上一点且AE=CD,连接AD,BE相交于点F.
求证:∠1=∠2.
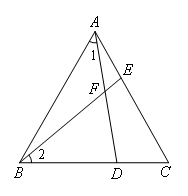
证明:如图,
在△ABD和△BCE中
∴△ABD≌△BCE(SAS)
∴
①BD=CE;②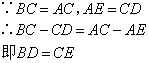 ;
;
③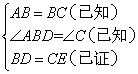 ;④
;④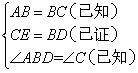 ;
;
⑤∠2=∠1(对应角相等);⑥∠1=∠2(全等三角形对应角相等).
以上空缺处依次所填最恰当的是( )
- A.①③⑥
- B.②④⑤
- C.②③⑥
- D.①④⑥
答案
正确答案:C
知识点:全等三角形的性质与判定
要证∠1=∠2,可以把∠1和∠2分别放在△ABD和△BCE中证全等;
全等要找三组条件,题中已经给出AB=BC,∠ABD=∠C这两组条件,
还需要再找一组条件.
根据题中给出的![]() ,可以证得边BD和CE相等,
,可以证得边BD和CE相等,
用SAS证明△ABD≌△BCE.
第一个空准备条件BD=CE,由题中给的![]() ,
,
可以证得BD=CE,故选②;
第二个空列全等的三组条件,利用的是SAS证明三角形全等,故选③;
第三个空填结论,理由是全等三角形对应角相等,故选⑥.
故选C
略








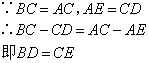 ;
;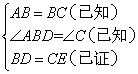 ;④
;④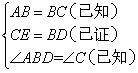 ;
;