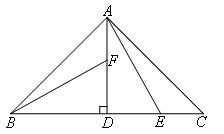
如图，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足为D；E，F分别是CD，AD上的点，且CE=AF．如果∠AED=62°，那么∠DBF=(    )

∵AB=AC，AD⊥BC，
∴BD=CD，∠ADB=∠ADC=90°，
∵∠BAC=90°，
∴AD=BD=CD，
∵CE=AF，
∴DF=DE，
∴△BDF≌△ADE（SAS）．
∴∠BFD=∠AED，
∵∠AED=62°，
∴∠BFD=62°，
∴∠DBF=28°．
故选C．

略