如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于点E，BD⊥AE交AE的延长线于点D，连接CD．下列结论：①AC+CE=AB；②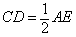；③∠CDA=45°．其中正确的结论序号有(    )

如图，延长AC交BD的延长线于点G．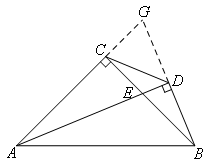

∵AD平分∠BAC
∴∠DAG=∠DAB
∵AD⊥BD
∴∠ADG=∠ADB
∴∠G=∠ABG
∴AB=AG
∴BD=GD
∵∠ACB=90°
∴∠BCG=90°
∴
∵∠G+∠DAG=90°，∠G+∠CBG=90°
∴∠DAG=∠CBG
在△ACE和△BCG中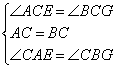

∴△ACE≌△BCG（ASA）
∴AE=BG，CE=CG
∴，AB=AG=AC+CG=AC+CE
故①②正确；
∵CD=BD
∴∠BCD=∠CBD，
∵∠CBD=∠CAE=∠BAE
∴∠BCD=∠BAE
∵∠DEC=∠BEA
∴∠CDA=∠ABC=45°，故③正确．
综上，正确的为①②③．
故选D．

略