如图，在平面直角坐标系中，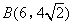
，BC⊥y轴于点C，点A在x轴正半轴上，且
∠OAB=45°．动点P从点C出发，以每秒2个单位长度的速度，沿折线CB—BA运动；动点Q从点A出发，以每秒1个单位长度的速度，向终点O运动，当一点停止运动时，另一点也停止运动．设点Q运动的时间为t秒．
（1）设△OPQ的面积为S，则S与t的关系式为( )
- A.
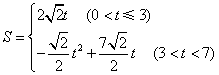
- B.
- C.
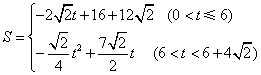
- D.
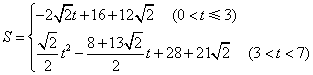
答案
正确答案：D
知识点：一次函数之动点问题
1．思路分析
①研究背景图形，如图（把函数信息转化为几何信息）
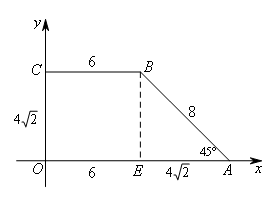
②分析运动过程，分段，定范围；
③根据路线图画图，表达，设计方案并计算．
2．解题过程：
如图，过点B作BE⊥x轴于点E，
∵
，
∴
，
∵
∴
，
，
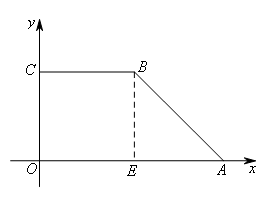
根据动点的运动情况，应该分为两段：
①当点P在线段BC上，即
时，如图：
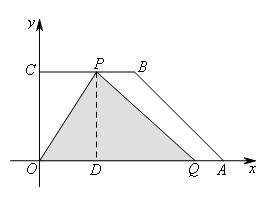
过点P作PD⊥x轴于点D，
∴
由动点的运动可知，
，
，
∴
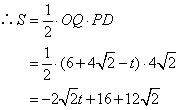
②当点P在线段AB上，即
时，如图：
过点P作PE⊥x轴于点E，
由动点的运动可知，
，，
∴
∵
∴
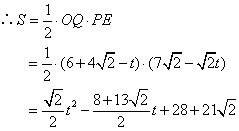
故选D．
略
WORD格式（
