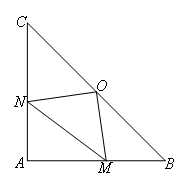
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.点M,N分别在线段AB,AC上移动,移动中保持AN=BM.若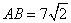 ,
,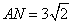 ,则OM的长为( )
,则OM的长为( )
- A.5
- B.4
- C.
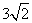
- D.
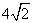
答案
正确答案:A
知识点:全等三角形的判定 勾股定理 直角三角形斜边上的中线等于斜边的一半 旋转的思想
如图,连接AO,
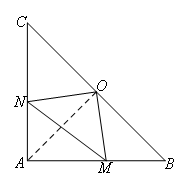
在Rt△ABC中,AB=AC,∠BAC=90°
∴∠C=∠B=45°
∵点O是BC的中点
∴AO=BO=CO,AO⊥BC
∴∠OAC=∠B=45°
∵AN=BM,
∴△ANO≌△BMO(SAS)
∴∠BOM=∠AON,ON=OM
∵∠BOM+∠AOM=90°
∴∠AON+∠AOM=90°
∴△OMN是等腰直角三角形
∵![]() ,
,![]()
∴![]()
在Rt△AMN中,∠BAC=90°
∴![]()
∴![]()
故选A.
略








