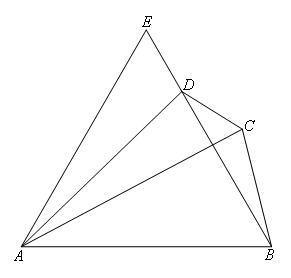
如图，在四边形ABCD中，AB=AC，∠ABD=60°，∠ADB=76°，∠BDC=28°，延长BD至点E，使得DE=DC，连接AE，则∠DBC的度数为(    )

∵∠ADB=76°
∴∠ADE=104°
∵∠BDC=28°
∴∠ADC=104°
∴∠ADE=∠ADC
又∵DE=DC，AD=AD，
∴△ADE≌△ADC（SAS），
∴AC=AE，
又∵AB=AC，∠ABD=60°，
∴△ABE是等边三角形，
∴∠DCA=∠E=60°，
设∠DBC=x，则∠ACB=∠ABC=60°+x，
在△BCD中，∠BDC+∠DCB+∠CBD=180°，
即28°+(60°+x+60°)+x=180°
解得x=16°，
∴∠DBC=16°．
故选B

略