如图,在平面直角坐标系xOy中,点P为抛物线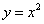 上一动点,点A的坐标为
上一动点,点A的坐标为
(4,2),若∠AOP=45°,则点P的坐标为( )
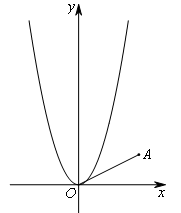
- A.
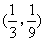
- B.(3,9)
- C.
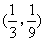 或(-3,9)
或(-3,9) - D.(3,9)或
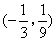
答案
正确答案:B
知识点:二次函数背景下的存在性问题 弦图模型
1.解题要点
①读题标注,理解题意
②分析特征有序思考,设计方案
分析定点,动点,找不变特征:
A,O为定点,点P是动点;射线OA固定,∠AOP=45°;
确定分类标准:
由题意,结合角的定义角是由两条具有公共端点的射线组成,
故在射线OA上方的抛物线上存在点P满足∠AOP=45°.
③根据方案作出图形,有序操作
要求点P的坐标,要充分利用∠AOP=45°,考虑放在直角三角形中;
以定点A为直角顶点构造直角三角形,借助弦图,转化为两个直角三角形相似(进一步的为全等)解决问题.
④求解验证
估算数值,对应图形判断结果是否正确,是否有其他未考虑的情况.
2.解题过程
略








