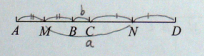
如图,B,C是线段AD上任意两点,M是AB的中点,N是CD的中点,若MN=a,BC=b,求证:AD=2a-b.

证明:如图,
∵M是AB的中点
∴
∵N是CD的中点
∴
∴AM+DN=BM+CN
=a-b
∴AD=AM+MN+DN
=a-b+a
=2a-b
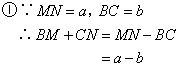 ;
;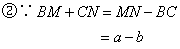 ;
;
③AM=BM;④BM=AM;⑤AB=2BM;⑥DN=CN;⑦CN=DN;⑧CD=2CN.
以上空缺处依次所填正确的是( )
- A.②⑤⑥
- B.①④⑧
- C.①③⑥
- D.②③⑦
答案
正确答案:C
知识点:中点的应用
先设计方案,把思路走通,再填写过程.
本题利用AD=AM+ND+MN=BM+CN+a=MN-BC+a=a-b+a=2a-b
求AD的长度.
根据题中证明的思路第一个空先利用MN=a,BC=b计算BM+CN;
第二个空已知BM,要求AM,利用AM=BM;
第三个空已知CN,要求DN,利用DN=CN.
所以,答案为①③⑥.
故选C.
略







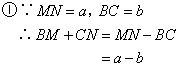 ;
;