如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M,N分别在AB,
AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=( )
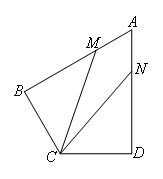
- A.
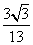
- B.
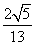
- C.
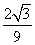
- D.
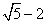
答案
正确答案:A
知识点:勾股定理 全等三角形的判定与性质
如图,连接AC,MN,过点M作ME⊥CN于点E,
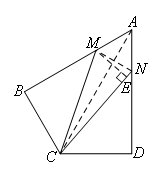
∵AB⊥BC,AD⊥CD,
∴∠ABC=∠ADC=90°,
∵AB=AD,AC=AC,
∴Rt△ABC≌Rt△ADC,
∴∠BAC=∠DAC.
∵∠BAD=60°,
∴∠BAC=∠DAC=30°,
∴![]() .
.
由题意,AM=AN=2,BM=DN=4,
∵∠BAD=60°,
∴△AMN为等边三角形,
∴MN=2.
在Rt△CBM中,![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∴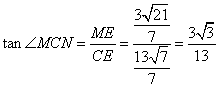 .
.
略








