某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
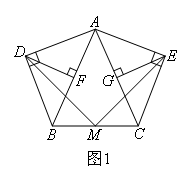
（1）操作发现：在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD，ME，则MD和ME具有怎样的数量关系和位置关系？请直接写出结论．

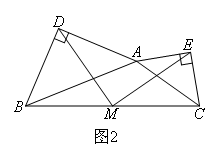
（2）数学思考：在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD，ME，则MD和ME具有怎样的数量关系和位置关系？请给出证明过程．

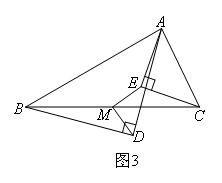
（3）类比探究：在任意△ABC中，分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD，ME，试判断△MED的形状．

（建议学生打印做题，并在做完之后对比解题思路中的过程，推敲里面是如何踩点得分的）
（1）中MD和ME之间的数量关系和位置关系分别是(    )

• A.MD=ME，MD与ME不垂直
• B.MD=ME，MD⊥ME
• C.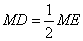，MD⊥ME
• D.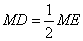，MD与ME不垂直

答案

正确答案：B

知识点：中考数学几何中的类比探究  

见第3题中解析

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>