已知:如图,△ABC和△CDE均为等腰直角三角形,∠ABC=∠CDE=90°,AB=BC,
DC=DE,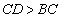 ,点C,B,D在同一直线上,F是AE的中点.
,点C,B,D在同一直线上,F是AE的中点.
求证:FD⊥FB,FD=FB.
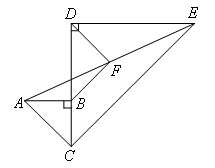
证明:如图,延长BF交DE于点G.
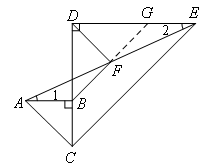
∴∠1=∠2
∵F是AE的中点
∴AF=EF
在△ABF和△EGF中

∴△ABF≌△EGF( )
∴AB=EG,BF=GF
∴DB=DG
∴△BDG为等腰直角三角形
∵BF=GF
∴DF⊥BF,∠BDF=∠GDF=45°
请你仔细观察下列序号所代表的内容:
①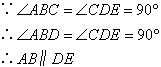 ;②
;②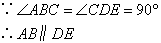 ;③AAS;④ASA;
;③AAS;④ASA;
⑤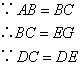 ;⑥∵DC=DE;⑦
;⑥∵DC=DE;⑦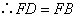 ;⑧
;⑧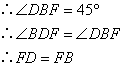 .
.
以上空缺处依次所填最恰当的是( )
- A.①④⑤⑧
- B.②④⑥⑦
- C.②③⑤⑦
- D.①③⑦⑧
答案
正确答案:A
知识点:全等三角形之倍长中线

略










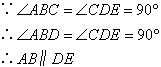 ;②
;②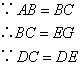 ;⑥∵DC=DE;⑦
;⑥∵DC=DE;⑦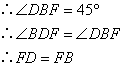 .
.