已知抛物线y=ax²+bx+c(a＜0)，顶点C的坐标为（1，-4），且与x轴交于A、B两点，A（-1，0）．
（1）求这条抛物线的解析式；
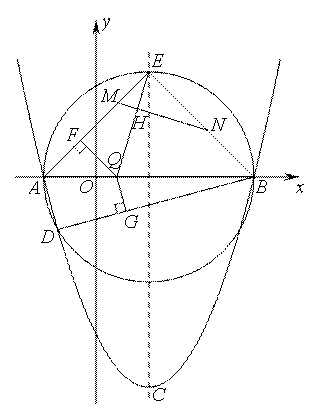
（2）如图，以AB为直径作圆，与抛物线交于点D，与抛物线的对称轴交于E，依次连接A、D、B、E，点Q为AB上一个动点（Q与A、B两点不重合），过点Q作QF⊥AE于F，QG⊥DB于G，请判断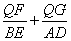是否为定值，若是，请求出此定值，若不是，请说明理由；
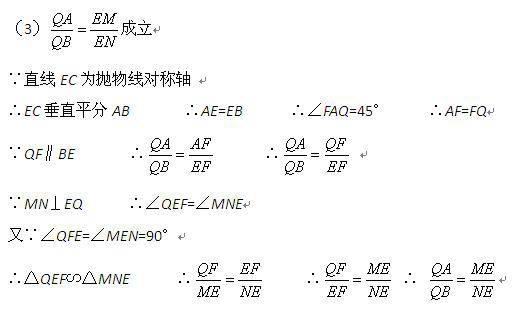
（3）在（2）的条件下，若点H是线段EQ上一点，过点H作MN⊥EQ，MN分别与边AE、BE相交于M、N（M与A、E不重合，N与E、B不重合），请判断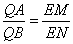是否成立，若成立，请给出证明，若不成立，请说明理由．

答案

（1）该抛物线的解析式为  
（2）的值为定值1.
（3）成立

知识点：中考压轴之定值问题  

解：（1）设抛物线解析式为将A（-1，0）代入得∴,即

 
            

略

下载次数：9

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>