压轴题专项训练（五）-九年级试卷-众享学科测评

压轴题专项训练（五）

满分100分答题时间30分钟

已经有507位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题16分) 如图，分别以菱形BCED的对角线BE，CD所在直线为x轴、y轴建立平面直角坐标系，抛物线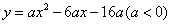过B，C两点，与x轴的负半轴交于点A，且∠ACB=90°．P是x轴上一动点，设点P的坐标为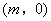，过点P作直线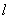⊥x轴，交抛物线于点Q． （1）求抛物线的解析式． （2）当点P在线段OB上运动时，直线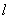交BD于点M．当m为何值时，四边形CQBM的面积最大？并求出这个最大值． （3）当点P在线段EB上运动时，若△BDQ为直角三角形，请直接写出此时点Q的坐标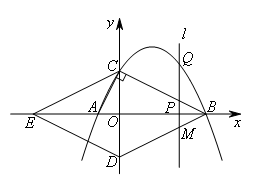． （建议学生打印做题，并在做完之后对比解题思路中的示范照片） 1．（1）中抛物线的解析式为( )

2.(本小题17分) 2．（上接第1题）（2）中四边形CQBM面积的最大值以及此时m的值分别为( )

3.(本小题17分) 3．（上接第1，2题）（3）中点Q的坐标为( )

4.(本小题16分) 已知：如图，在四边形OABC中，AB∥OC，BC⊥x轴于点C，，动点P从点O出发，沿着x轴正方向以每秒2个单位长度的速度移动．过点P作PQ垂直于直线OA，垂足为点Q，设点P移动的时间为t秒（），△OPQ与四边形OABC重叠部分的面积为S． （1）求经过O，A，B三点的抛物线的解析式； （2）将△OPQ绕着点P按逆时针方向旋转90°，若△OPQ的顶点O或顶点Q在抛物线上，请求出符合题意的t值； （3）求出S与t之间的函数关系式． （建议学生打印做题，并在做完之后对比解题思路中的示范照片） 1．（1）中过O，A，B三点的抛物线解析式为( )

5.(本小题17分) 2．（上接第4题）（2）中符合题意的t值为( )

6.(本小题17分) 3．（上接第4，5题）（3）中S与t之间的函数关系式为( )