全等三角形之辅助线(北师版)
满分100分 答题时间30分钟
已经有534位用户完成了练习
单选题(本大题共小题, 共分)
-
4.(本小题20分)
已知:如图,OP平分∠AOB,C,D分别在OA,OB上,若∠PCO+∠PDO=180°.
求证:PC=PD.
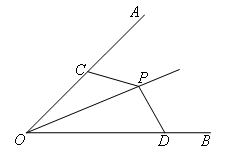
证明:如图,过点P作PE⊥OA于点E,PF⊥OB于点F.
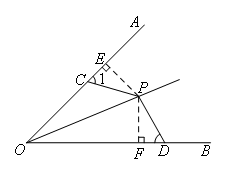
∵OP平分∠AOB,PE⊥OA,PF⊥OB
∴
∠PEC=∠PFD=90°
∵∠PCO+∠PDO=180°
∠PCO+∠1=180°
∴
在△PEC和△PFD中
∴△PEC≌△PFD(AAS)
∴PC=PD
请你仔细观察下列序号所代表的内容:
①PE=PF;②∠EOP=∠FOP;③∠EPC=∠FPD;④∠1=∠PDO;
⑤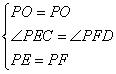 ;⑥
;⑥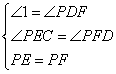 .
.
以上空缺处依次所填最恰当的是( )
核心考点: 全等三角形的性质 全等三角形的判定 角平分线性质定理





 ;
; ;⑤SAS;⑥SSA.
;⑤SAS;⑥SSA.

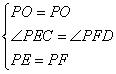 ;⑥
;⑥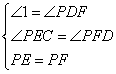 .
.

 ;
; ;⑦
;⑦ ;⑧
;⑧
