2012年郑州市九年级第二次质量预测数学模拟卷(一)
满分120分 答题时间100分钟
已经有623位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
18.(本小题9分)
某区共有甲、乙、丙三所初中,所有九年级学生参加了一次数学测试.老师们对其中的一道题进行了分析,把每个学生的解答情况归结为下列四类情况之一:A--概念错误;B--计算错误;C--解答基本正确,但不完整;D--解答完全正确.各校出现这四类情况的人数分别占本校九年级学生数的百分比如下表所示:
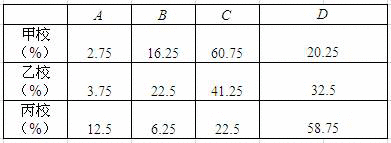
已知甲校九年级有400名学生,这三所学校九年级学生人数的扇形统计图如图所示:
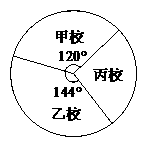
根据以上信息,解答下列问题:
(1)求全区九年级学生总数;
(2)求全区解答完全正确的学生数占全区九年级学生总数的百分比m(精确到0.01%);
(3)请你对表中三校的数据进行对比分析,给丙校九年级数学老师提一个值得关注的问题,并说明理由.
核心考点: 统计表 扇形统计图
-
23.(本小题12分)
如图,直角梯形OABC中,AB∥OC,∠OAB=90°且OA=AB,点A、C的坐标分别为(0,3)、(4,0),动点P从O点出发,沿线段OC向点C作匀速运动;动点Q从点B出发,沿线段BA向点A作匀速运动.过Q点垂直于AB的射线交AC于点M,交OC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
(1)求NC,MC的长(用含t的代数式表示);
(2)当t为何值时,四边形PCBQ构成平行四边形?
(3)是否存在某一时刻,使射线QN恰好将△AOC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;
(4)探究:t为何值时,△PMC为等腰三角形.
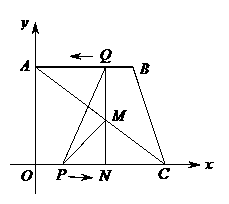
核心考点: 二次函数综合题 等边三角形的性质 勾股定理 直角梯形 平行四边形的性质(对边相等)




 的结果是 .
的结果是 .

 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .



 .其中x=-3,y=-2.
.其中x=-3,y=-2.




 ,tan8°≈
,tan8°≈ ,sin10°≈
,sin10°≈ ,tan10°≈
,tan10°≈ )
)