2011-2012学年七年级下册数学期末考试模拟卷（二）北师版-七年级试卷-众享学科测评

学科测评首页

2011-2012学年七年级下册数学期末考试模拟卷（二）北师版

满分100分答题时间90分钟

已经有1640位用户完成了练习

本试卷为的课后练习题

单选题(本大题共小题，共分)

1.(本小题3分) 下列计算正确的是（）

2.(本小题3分) 在平面内用9根牙签首尾顺次相接（全用上且不折断）搭成三角形，能搭成（）种不同的三角形

3.(本小题3分) 如图，CA⊥BE于A，AD⊥BF于D，下列说法正确的是（）

4.(本小题3分) 从《中华人民共和国2011年国民经济和社会发展统计报告》中获悉，去年我国国内生产总值达到471564亿元，请你以亿元为单位用科学记数法表示去年我国的国内生产总值为（结果保留三个有效数字）（）

5.(本小题3分) 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（）

6.(本小题3分) 某天，小明走路去学校，开始他以较慢的速度匀速前进，然后他越走越快走了一段时间，最后他以较快的速度匀速前进达到学校．小明走路的速度v（米/分钟）与时间t（分钟）的关系图象是（）

填空题(本大题共小题，共分)

7.(本小题3分)

8.(本小题3分) 在代数式a，π，，a-b，，，中次数为2的单项式是 .

9.(本小题3分) 当x=﹣3时，y=7，那么当x=3时，y的值是 .

10.(本小题3分) 如图，随意掷一枚正方体骰子，均落在图中的小方格内（每个方格除颜色外完全相同），那么这枚骰子落在图中阴影小方格中的概率为_．

11.(本小题3分) 如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为_.

12.(本小题3分) 已知△ABC三条边都不相等，P是△ABC所在平面上一点，P不与点A重合且又不在直线BC上，要想使△PBC与△ABC全等，则这样的P点有个．

13.(本小题3分) 如图（1）所示，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为x，△ABP的面积为y，如果y与x的关系图象如图（2）所示，那么△ABC的面积是_．

14.(本小题3分) 如图，在△ABC中，AB=AC，BD=CD，∠BAD=24°，AE=AD，则∠EDC的度数是_．

15.(本小题3分) 如图，点D、E在△ABC的BC边上，∠BAD=∠CAE，要推理得出△ABE≌△ACD，可以补充的一个条件是（不添加辅助线，写出一个即可）_．

解答题(本大题共小题，共分)

16.(本小题6分) 如图，阴影部分是由5个小正方形组成的一个直角图形，请用三种方法分别在下图方格内添涂黑两个小正方形，使它们成为轴对称图形．

17.(本小题7分) 先化简再求值：，其中a=-3，b=2.

18.(本小题9分) 如图，BC与DE相交于O点，给出下列三个判断：①∠B=∠E，②AB∥DE，③BC∥EF．请以其中两个论断为条件，一个论断为结论，编一道证明题，并加以证明． 已知：____（填序号） 求证：____（填序号）

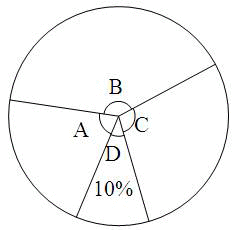
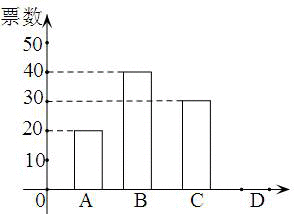
19.(本小题10分) “五•一”假期，某公司组织部分员工分别到A、B、C、D四地旅游，公司按定额购买了前往各地的车票．下图是未制作完的车票种类和数量的条形统计图，根据统计图回答下列问题： （1）根据扇形统计图，将条形统计图补全； （2）求到A地旅游的人数占该公司全部旅游员工的百分比； （3）若公司采用随机抽取的方式分发车票，每人抽取一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么员工小胡抽到去A地的概率是多少？ （4）若有一张车票，小王、小李都想要，决定采取抛掷一枚各面分别标有1，2，3，4的正四面体骰子的方法来确定，请你设计游戏规则，使得到车票的可能性相等.

20.(本小题11分) 小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 min才乘上缆车，缆车的平均速度为180 m/min．设小亮出发x min后行走的路程为y m．图中的折线表示小亮在整个行走过程中y与x的变化关系． （1）小亮行走的总路程是 m，他途中休息了 min． （2）①在BC段的时候，求变量x与y之间的关系表达式； ②当小颖到达缆车终点时，小亮离缆车终点的路程是多少？

证明题(本大题共小题，共分)

21.(本小题12分) 如图，CD是经过∠BCA顶点C的一条直线，且直线CD经过∠BCA的内部，点E，F在射线CD上，已知CA=CB且∠BEC=∠CFA=∠α． （1）如图1，若∠BCA=90°，∠α=90°，问EF=BE-AF，成立吗？说明理由． （2）将（1）中的已知条件改成∠BCA=60°，∠α=120°（如图2），问EF=BE-AF仍成立吗？说明理由． （3）若0°＜∠BCA＜90°，请你添加一个关于∠α与∠BCA关系的条件，使结论EF=BE-AF仍然成立．你添加的条件是．（直接写出结论） （4）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．

上一讲: 下一讲: