九年级数学上学期阶段综合练习(一)(九上全部)(北师版)
满分120分 答题时间100分钟
已经有38位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
22.(本小题10分)
如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B,C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C,D)以每秒1个单位长度的速度,匀速向点D运动;点E,F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD的延长线于点N,连接MN.设运动时间为t秒.
(1)当t为何值时,△ABE∽△ECF;
(2)在点E运动的过程中是否存在某个时刻使AE⊥AN?若存在,请求出t的值;若不存在,请说明理由;
(3)在运动的过程中,△AMN的面积是否变化?如果改变,求出变化的范围;如果不变,求出它的值.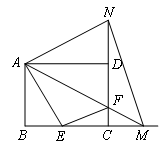
核心考点: 相似三角形的判定与性质 存在性问题