九年级数学 投影与视图单元练习(二)(人教版)
满分120分 答题时间100分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
23.(本小题11分)
如图,平面内的两条直线
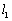 ,
, ,点A,B在直线
,点A,B在直线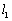 上,点C,D在直线
上,点C,D在直线 上,过A,B两点分别作直线
上,过A,B两点分别作直线 的垂线,垂足分别为A1,B1,我们把线段A1B1叫做线段AB在直线
的垂线,垂足分别为A1,B1,我们把线段A1B1叫做线段AB在直线 上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线
上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线 上的正投影就是线段A1C.
上的正投影就是线段A1C.
请依据上述定义解决如下问题:
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).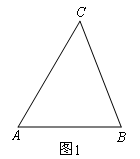


核心考点: 正投影





























