八年级数学数据的分析单元练习（一）（北师版）-八年级试卷-众享学科测评

天天练

八年级数学数据的分析单元练习（一）（北师版）

满分120分答题时间100分钟

已经有3位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 已知某同学近几次的数学成绩分别为92，90，88，92，93，则该同学这几次数学成绩的平均数和众数分别是( )

2.(本小题3分) 为了提高班级凝聚力，班长计划周末带全班同学去看电影，现对全班同学喜欢看的电影做了民意调查，然后决定看什么电影，那么最值得关注的应该是统计调查数据的( )

3.(本小题3分) 某中学随机地调查50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示： 则这50名学生这一周在校的平均体育锻炼时间是( )

4.(本小题3分) 下列说法错误的是( )

5.(本小题3分) 对于数据2，2，3，2，5，2，10，2，5，2，3，下列说法正确的有( ) ①众数是2； ②众数与中位数的数值不相等； ③中位数与平均数的数值相等； ④平均数与众数的数值相等．

6.(本小题3分) （2021鄂尔多斯）小明收集了鄂尔多斯市某酒店2021年3月1日-3月6日每天的用水量（单位：吨），整理并绘制成如图所示的折线统计图，下列结论正确的是( )

7.(本小题3分) 某排球队6名场上队员的身高（单位：cm）是：180，184，188，190，192，194．现用一名身高为186 cm的队员换下场上身高为192 cm的队员，与换人前相比，场上队员的身高( )

8.(本小题3分) 国家规定“中小学生每天在校体育活动时间不低于1小时”．为此，我市就“你每天在校体育活动时间是多少”的问题随机调查了某区300名初中学生．根据调查结果绘制成的统计图如图所示，其中分组情况是：A组：t<0.5 h；B组：0.5 h≤t<1 h；C组：1 h≤t<1.5 h；D组：t≥1.5 h． 根据上述信息，你认为本次调查数据的中位数落在( )

9.(本小题3分) 初三体育素质测试，某小组5名同学成绩如下所示，有两个数据被遮盖，如图： 那么被遮盖的两个数据依次是( )

10.(本小题3分) 若样本x₁+1，x₂+1，…，x_n+1的平均数为10，方差为2，则对于样本x₁+2，x₂+2，…，x_n+2，下列结论正确的是( )

填空题(本大题共小题，共分)

11.(本小题4分) 数据1，5，6，5，6，5，6，6的众数是____，方差是____．

12.(本小题3分) （2021北京）有甲、乙两组数据，如下表所示： 甲、乙两组数据的方差分别为s²_甲，s²_乙，则s²_甲____s²_乙（填“＞”，“<”或“=”）．

13.(本小题3分) 某公司对应聘者进行面试，按专业知识、工作经验、仪表形象给应聘者打分，这三个方面的重要性之比为6：3：1．对应聘的王丽、张瑛两人的打分如下，如果两人中只录取一人，若你是人事主管，你会录用____．

14.(本小题3分) 小明等五名同学四月份参加某次数学测验的成绩如下：100，100，x，x，80．已知这组数据的中位数和平均数相等，那么整数x的值为____．

15.(本小题3分) 若干名同学制作迎世乒卡通图片，他们制作的卡通图片张数的条形统计图如图所示，设他们制作的卡通图片张数的平均数为a，中位数为b，众数为c，则a，b，c的大小关系为____．（按从大到小的顺序）

解答题(本大题共小题，共分)

16.(本小题6分) 有七个数由小到大依次排列，其平均数是38，如果这组数的前四个数的平均数是33，后四个数的平均数是42．求它们的中位数．

17.(本小题8分) 甲、乙两位同学参加数学综合素质测试，各项成绩如下： （1）分别计算甲、乙成绩的中位数； （2）如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算，那么甲、乙的数学综合素质成绩分别为多少分？

18.(本小题9分) 课外兴趣小组为了解某段路上机动车的车速，抽查了一段时间内若干辆车的车速（车速取整数，单位：千米/时），并制成如图所示的频数分布直方图．已知车速在41千米/时到50千米/时的车辆数占车辆总数的． （1）在这段时间中他们抽查的车有辆． （2）被抽查车辆的车速的中位数所在速度段（单位：千米/时）是( ) A．30.5∼40.5B．40.5∼50.5C．50.5∼60.5D．60.5∼70.5 （3）补全频数分布直方图．

19.(本小题10分) （2021包头）为了庆祝中国共产党建党100周年，某校开展了学党史知识竞赛．参加知识竞赛的学生分为甲、乙两组，每组学生均为20名，赛后根据竞赛成绩得到尚不完整的统计图表（如图），已知竞赛成绩满分为100分，统计表中a，b满足b=2a． 请根据所给信息，解答下列问题： （1）求统计表中a，b的值； （2）根据所学统计知识判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果； （3）如果依据平均成绩确定竞赛结果，那么竞赛成绩较好的是哪个组？请说明理由．

20.(本小题10分) （2021河南）2021年4月，教育部印发《关于进一步加强中小学生睡眠管理工作的通知》，明确要求初中生每天睡眠时间应达到9小时．某初级中学为了解学生睡眠时间的情况，从本校学生中随机抽取500名进行问卷调查，并将调查结果用统计图描述如下． 根据以上信息，解答下列问题： （1）本次调查中，平均每天睡眠时间的中位数落在第（填序号）组，达到9小时的学生人数占被调查人数的百分比为； （2）请对该校学生睡眠时间的情况作出评价，并提出两条合理化建议．

21.(本小题10分) （2021广州）某中学为了解初三学生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下： 3，5，3，6，3，4，4，5，2，4，5，6，1，3，5，5，4，4，2，4． 根据以上数据，得到如下不完整的频数分布表： （1）表格中的a= ，b= ； （2）在这次调查中，参加志愿者活动的次数的众数为，中位数为； （3）若该校初三年级共有300名学生，根据调查统计结果，估计该校初三年级学生参加志愿者活动的次数为4次的人数．

22.(本小题10分) 在一组数据x₁，x₂，…，x_n中，各数据与它们的平均数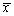的差的绝对值的平均数，即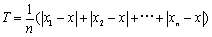叫做这组数据的“平均差”．“平均差”也能描述一组数据的离散程度．“平均差”越大说明数据的离散程度越大．因为“平均差”的计算要比方差的计算容易一点，所以有时人们也用它来代替方差来比较数据的离散程度．极差、方差（标准差）、平均差都是反映数据离散程度的量． 一水产养殖户李大爷要了解鱼塘中鱼的重量的离散程度，因为个头大小差异太大会出现“大鱼吃小鱼”的情况．为防止出现“大鱼吃小鱼”的情况，在能反映数据离散程度的几个量中某些值超标时就要捕捞，分开养殖或出售．他从两个鱼塘各随机捕捞10条鱼称得重量如下（单位：千克）： A鱼塘：3，5，5，5，7，7，5，5，5，3； B鱼塘：4，4，5，6，6，5，6，6，4，4． （1）分别计算A、B两个鱼塘中抽取的样本的极差、方差、平均差，完成下面的表格： （2）如果你是技术人员，你会建议李大爷注意哪个鱼塘的风险更大些？计算哪些量更能说明鱼重量的离散程度？

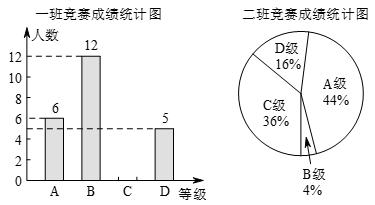
23.(本小题11分) 6月5日是世界环境日，某校组织了一次环保知识竞赛，每班选25名同学参加比赛，成绩分别为A，B，C，D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将某年级的一班和二班的成绩整理并绘制成如下统计图： 根据以上提供的信息解答下列问题： （1）把一班竞赛成绩统计图补充完整； （2）写出下表中a，b，c的值： （3）请从以下给出的三个方面对这次竞赛成绩的结果进行分析： ①从平均数和中位数方面比较一班和二班的成绩； ②从平均数和众数方面比较一班和二班的成绩； ③从B级以上（包括B级）的人数方面来比较一班和二班的成绩．

八年级数学 数据的分析单元练习（一）（北师版）

单选题(本大题共小题， 共分)

填空题(本大题共小题， 共分)

解答题(本大题共小题， 共分)

八年级数学数据的分析单元练习（一）（北师版）

单选题(本大题共小题，共分)

填空题(本大题共小题，共分)

解答题(本大题共小题，共分)