九年级数学 圆单元练习(一)(北师版)
满分120分 答题时间100分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
22.(本小题11分)
若一直线与圆相交,过交点作圆的切线,则此切线与直线的交角中的任意一个称为直线和圆的交角,其中所夹弧为劣弧的角为劣交角,所夹弧为优弧的角为优交角.直线和圆的交角有以下性质:直线和圆的交角等于所夹弧所对的圆周角.
(1)为了说明直线和圆的交角性质的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程(只证明劣交角即可).
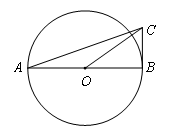
已知:如图1,直线 与⊙O相交于点A,B,过点B作 .
与⊙O相交于点A,B,过点B作 .
求证:∠ABD= .
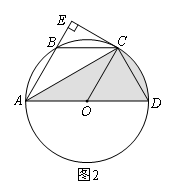
(2)如图2,直线 与⊙O相交于点A,B,AD为⊙O的直径,BC切⊙O于点B,交DA的延长线于点C,若AD=BC,AC=2,求⊙O的半径.
与⊙O相交于点A,B,AD为⊙O的直径,BC切⊙O于点B,交DA的延长线于点C,若AD=BC,AC=2,求⊙O的半径.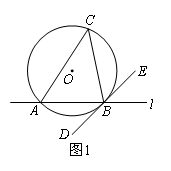

核心考点: 圆周角定理 切线的性质