九年级数学解直角三角形单元练习（二）（冀教版）-九年级试卷-众享学科测评

九年级数学解直角三角形单元练习（二）（冀教版）

满分120分答题时间100分钟

已经有0位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 在Rt△ABC中，∠C=90°，在下列条件中不能解直角三角形的是( )

2.(本小题3分) 如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，设∠ABC=α，则下列结论错误的是( )

3.(本小题3分) 如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′处，那么tan∠BAD′等于( )

4.(本小题3分) 在△ABC中，∠C是直角，，则sinB=( )

5.(本小题3分) 已知α为锐角，且，则α=( )

6.(本小题3分) （2021金华）如图是一架人字梯，已知AB=AC=2米，AC与地面BC的夹角为α，则两梯脚之间的距离BC为( )

7.(本小题3分) 如图，长方形纸片的宽为1，沿直线BC折叠，得到重合部分△ABC，∠BAC=30°，则△ABC的面积为( )

8.(本小题3分) （2021随州）如图，某梯子长10米，斜靠在竖直的墙面上，当梯子与水平地面所成角为α时，梯子顶端靠在墙面上的点A处，底端落在水平地面的点B处，现将梯子底端向墙面靠近，使梯子与地面所成角为β，已知sinα=cosβ=，则梯子顶端上升了( )

9.(本小题3分) 如图，在2×2的网格中，以顶点O为圆心，以2个单位长度为半径作圆弧，交图中格线于点A，则tan∠ABO的值为( )

10.(本小题3分) （2021绍兴）如图，Rt△ABC中，∠BAC=90°，，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使∠ADE=∠B，连接CE，则的值为( )

填空题(本大题共小题，共分)

11.(本小题3分) 一轮船以每小时20海里的速度沿正东方向航行，上午8时，该船在A处测得某灯塔位于北偏东30°的B处，上午9时行至C处，测得灯塔恰好在它的正北方向，此时它与灯塔的距离是____海里（结果保留根号）．

12.(本小题3分) 如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为____．

13.(本小题3分) 如图，在四边形ABCD中，∠B=90°，AB=2，CD=8，AC⊥CD．若，则tanD=____．

14.(本小题3分) 如图，点A(3，t)在第一象限，OA与x轴所夹的锐角为α，，则t的值是____．

15.(本小题3分) 如图，在△ABD中，点C为BD的中点，连接AC，点E在AC上，连接BE，若AB=AC，，∠BAC=2∠EBC，BC=，则AD的长为____．

解答题(本大题共小题，共分)

16.(本小题8分) 求下列各式的值． （1）；（2）．

17.(本小题8分) 如图，一条城际铁路从A市到B市需要经过C市，A市位于C市西南方向，与C市相距40千米，B市恰好位于A市的正东方向和C市的南偏东60°方向处．因打造城市经济新格局需要，将从A市到B市之间铺设一条笔直的铁路，求新铺设的铁路AB的长度．（结果保留根号）

18.(本小题9分) （2021上海）如图，已知△ABD中，AC⊥BD，BC=8，CD=4，cos∠ABC=，BF为AD边上的中线． （1）求AC的长； （2）求tan∠FBD的值．

19.(本小题9分) （2021贵阳）随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量广场B，C两点之间的距离．如图所示，小星站在广场的B处遥控无人机，无人机在A处距离地面的飞行高度是41.6 m，此时从无人机测得广场C处的俯角为63°，他抬头仰视无人机时，仰角为α，若小星的身高BE=1.6 m，EA=50 m（点A，E，B，C在同一平面内）． （1）求仰角α的正弦值； （2）求B，C两点之间的距离（结果精确到1m）． （sin63°≈0.89，cos63°≈0.45，tan63°≈1.96，sin27°≈0.45，cos27°≈0.89，tan27°≈0.51）

20.(本小题10分) 通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角正对（sad），如图1，在△ABC中，AB=AC，顶角A的正对记作sadA，容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题： （1）sad 60°= ； （2）对于0°<A<180°，∠A的正对值sadA的取值范围是； （3）如图2，已知，其中∠A为锐角，试求sadA的值．

21.(本小题10分) （2021江西）图1是疫情期间测温员用“额温枪”对小红测温时的实景图，图2是其侧面示意图，其中枪柄BC与手臂MC始终在同一直线上，枪身BA与额头保持垂直．量得胳膊MN=28 cm，MB=42 cm，肘关节M与枪身端点A之间的水平宽度为25.3 cm（即MP的长度），枪身BA=8.5 cm． （1）求∠ABC的度数； （2）测温时规定枪身端点A与额头距离范围为3~5 cm．在图2中，若测得∠BMN=68.6°，小红与测温员之间距离为50 cm．问此时枪身端点A与小红额头的距离是否在规定范围内？并说明理由．（结果保留小数点后一位）（参考数据：sin66.4°≈0.92，cos66.4°≈0.40，sin23.6°≈0.40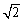，≈1.414）

22.(本小题10分) （2021永州）已知锐角△ABC中，角A，B，C的对边分别为a，b，c，边角总满足关系式：． （1）如图1，若a=6，∠B=45°，∠C=75°，求b的值； （2）某公园准备在园内一个锐角三角形水池ABC中建一座小型景观桥CD（如图2所示），若CD⊥AB， AC=14米，AB=10米，，求景观桥CD的长度．

23.(本小题11分) 如图，已知等腰直角三角形ABC中，D，E，F分别为边AB，AC，BC的中点，点M为斜边BC所在直线上一动点，且三角形DMN为等腰直角三角形（DM=DN，D，M，N呈逆时针）． （1）如图1点M在边BC上，判断MF和AN的数量和位置关系，请直接写出你的结论． （2）如图2点M在B点左侧时；如图3，点M在C点右侧．其他条件不变，（1）中结论是否仍然成立，并选择图2或图3的一种情况来说明理由． （3）在图2中若∠DMB=α，连接EN，请猜测MF与EN的数量关系，即MF= EN．（用含α的三角函数的式子表示）