【中考压轴题】十大类型之函数类问题专项备考练习
满分100分 答题时间30分钟
已经有148位用户完成了练习
解答题(本大题共小题, 共分)
-
1.(本小题50分)
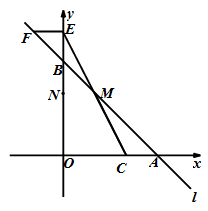
已知直线l:y=-x+m(m≠0)交x轴、y轴于A、B两点,点C、M分别在线段OA、AB上,且OC=2CA,AM=2MB,连接MC,将△ACM绕点M旋转180°,得到△FEM,则点E在y轴上,点F在直线l上;取线段EO中点N,将△ACM沿MN所在直线翻折,得到△PMG,其中P与A为对称点.记:过点F的双曲线为C1,过点M且以B为顶点的抛物线为C2,过点P且以M为顶点的抛物线为C3.(1)如图,当m=6时,①直接写出点M、F的坐标,②求C1、C2的函数解析式;
(2)当m发生变化时,①在C1的每一支上,y随x的增大如何变化?请说明理由.②若C2、C3中的y都随着x的增大而减小,写出x的取值范围.
核心考点: 函数与方程思想
-
2.(本小题50分)
(2011浙江温州)如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C,记点P关于y轴的对称点为P′ (点P′不在y轴上),连结PP′,P′A,P′C,设点P的横坐标为a.
(1)当b=3时,①直线AB的解析式;②若点P′的坐标是(-1,m),求m的值;
(2)若点P在第一象限,记直线AB与P′C的交点为D.当P′D:DC=1:3时,求a的值;
(3)是否同时存在a,b,使△P′CA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由.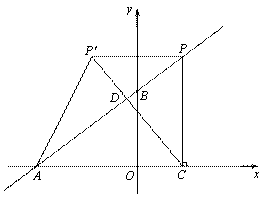
核心考点: 函数与方程思想
上一讲:
下一讲:



