【中考数学压轴题】十大类型之三角形的存在性问题备考练习
满分100分 答题时间40分钟
已经有83位用户完成了练习
解答题(本大题共小题, 共分)
-
2.(本小题50分)
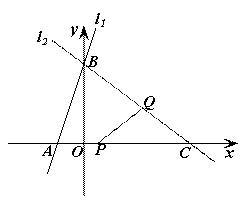
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴相交于点C.连结AC、BC,A、C两点的坐标分别为A(-3,0)、C
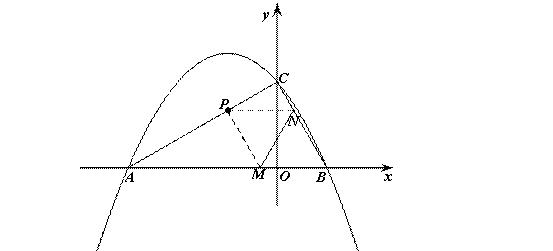
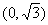 ,且当x=-4和x=2时二次函数的函数值y相等.(1)求实数a、b、c的值;(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t秒时,连结MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值及点P的坐标;(3)在(2)的条件下,二次函数图象的对称轴上是否存在点Q,使得以B,N,Q为顶点的三角形与△ABC相似?如果存在,请求出点Q的坐标;如果不存在,请说明理由.
,且当x=-4和x=2时二次函数的函数值y相等.(1)求实数a、b、c的值;(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t秒时,连结MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值及点P的坐标;(3)在(2)的条件下,二次函数图象的对称轴上是否存在点Q,使得以B,N,Q为顶点的三角形与△ABC相似?如果存在,请求出点Q的坐标;如果不存在,请说明理由.
核心考点: 中考压轴之三角形存在性问题
上一讲:
下一讲: