类比探究练习（北师版）-八年级试卷-众享学科测评

类比探究练习（北师版）

满分100分答题时间30分钟

已经有782位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题12分) 如图，直线CD经过∠BCA的顶点C，点E，F在直线CD上，已知CA=CB，∠BEC=∠CFA=α． （1）如图1，若∠BCA=90°，α=90°，试证明EF=BE-AF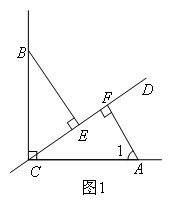． 解题思路：（1）由∠BCA=∠CFA=90°，可以得到∠BCE＋∠ACF＝90°，∠ACF+∠1=90°，得到，理由是．又因为CB=AC，∠BEC=∠CFA，因此根据全等三角形的判定定理，可以得到，由全等的性质得到CE=AF，BE=CF，最后得到EF=CF-CE=BE-AF． ①∠BCE=∠1；②∠BCE=∠ACF；③同角的余角相等；④同角的补角相等；⑤△BEC≌△AFC； ⑥△BEC≌△CFA；⑦AAS；⑧ASA． 以上横线处，依次所填正确的是( )

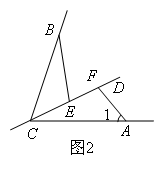
2.(本小题12分) （上接第1题）（2）如图2，若∠BCA=60°，α=120°，结论EF=BE-AF仍成立吗？若成立，请给出证明，若不成立，请说明理由.． 解题思路：（2）由∠BCA=60°，∠AFC=120°，可以得到∠BCE＋∠ACF＝60°，∠ACF+∠1=60°，得到，理由是．又因为CB=AC，∠BEC=∠CFA，因此根据全等三角形的判定定理，可以得到，由全等的性质得到CE=AF，BE=CF，最后得到EF=CF-CE=BE-AF． ①∠BCE=∠1；②∠BCE=∠ACF；③等式性质；④同角的余角相等；⑤△BEC≌△AFC；⑥△BEC≌△CFA；⑦AAS；⑧ASA． 以上横线处，依次所填正确的是( )

3.(本小题12分) （上接第1，2题）（3）如图3，若0°<∠BCA<90°，若让你添加一个关于∠α与∠BCA的条件，使结论EF=BE-AF仍然成立，则你添加的条件是( )

4.(本小题12分) 在正方形ABCD中，P是直线CD上一点，连接PA，分别过点B，D作BE⊥PA，DF⊥PA，垂足分别为点E，F． （1）如图，当点P在边CD上时，BE，DF，EF这三条线段之间的数量关系为( )

5.(本小题13分) （上接第4题）（2）如图，当点P在DC的延长线上时，BE，DF，EF这三条线段之间的数量关系为( )

6.(本小题13分) （上接第4，5题）（3）如图，当点P在CD的延长线上时，BE，DF，EF这三条线段之间的数量关系为( )

7.(本小题13分) 如图1，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°， 连接EF．利用旋转的思想很容易证明DE+BF=EF； 如图2，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且． 则DE，BF，EF之间的数量关系为( )

8.(本小题13分) （上接第7题）如图3，在四边形ABCD中，AB=AD，E，F分别为DC，BC边上的点，且满足，当∠ABC与∠ADC满足( )时，可使得DE+BF=EF．