如图，在△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，垂足分别为D，E．
若∠AFD=158°，则∠EDF=(    )

读题标注，如图：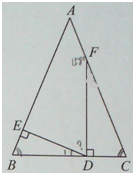

由FD⊥BC，DE⊥AB，可得∠BED=∠FDB=∠FDC=90°，
∠AFD可以看作△FDC的一个外角，则∠C=∠AFD－∠FDC＝158°－90°=68°，
结合∠B=∠C，因此∠B=68°，
因为∠BED=∠FDB=90°，
所以∠B+∠1=90°，∠EDF+∠1=90°
由同角的余角相等，得∠B=∠EDF
因此∠EDF=68°
故选C．

略