已知抛物线 $\footnotesize y=-\frac{1}{3}x^{2}+\frac{4}{3}x+\frac{5}{3}$ ，求：
（1）把它配方成 $\footnotesize y=a(x-h)^{2}+k$ 形式；
（2）写出它的顶点M的坐标、对称轴和最值；
（3）求出图象与x轴的交点坐标A、B；
（4）作出函数图象；根据图象指出x取什么值时y＞0；
（5）求△AMB面积．

答案

（1） $\footnotesize y=-\frac{1}{3}(x-2)^{2}+3$ ；（2）M（2,3），对称轴为x=2，最大值为3；（3）（-1,0）、（5,0）；（4）x取-1＜x＜5时，y＞0；（5）9

（1）由a= $\footnotesize -\frac{1}{3}$ ，b= $\footnotesize \frac{4}{3}$ ，c= $\footnotesize \frac{5}{3}$ 可得 $\footnotesize -\frac{b}{2a}$ =2， $\footnotesize \frac{4ac-b^{2}}{4a}$ =3，所以抛物线的一般式可以配方成 $\footnotesize y=-\frac{1}{3}(x-2)^{2}+3$ .
（2）根据（1）中的计算可知顶点M的坐标为（2,3），对称轴为x=2，最大值为3.
（3）由 $\footnotesize y=-\frac{1}{3}x^{2}+\frac{4}{3}x+\frac{5}{3}$ =0得，x=-1或x=5，所以图象与x轴的交点A、B的坐标分别为（-1,0）、（5,0）.
（4）函数图象如下：

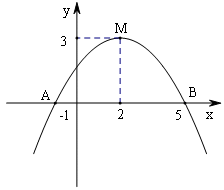
由图象可以看出x取-1＜x＜5时，y＞0
（5）|AB|=5-（-1）=6，M到x轴的距离为3， $\footnotesize S_{\triangle AMB}$ = $\footnotesize \frac{1}{2}$ ×6×3=9.