（2010重庆改编）等边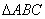
的两边AB、AC所在直线上分别有两点M、N，D为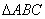外一点，且
,
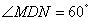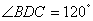,BD=DC.探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及
的周长Q与等边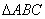的周长L的关系．
（I）如图1，当点M、N在边AB、AC上，且DM=DN时，BM、NC、MN之间的数量关系是_____________；此时
___________；
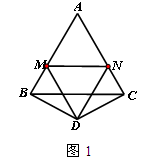
（II）如图2，点M、N在边AB、AC上，且当DM
DN时，猜想（I）问的两个结论还成立吗？写出你的猜想并加以证明；
（III）如图3，当M、N分别在边AB、CA的延长线上时，若AN=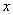
，则Q=_________（用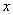、L表示）．
的两边AB、AC所在直线上分别有两点M、N，D为
,
,BD=DC.探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及
的周长Q与等边
___________；
DN时，猜想（I）问的两个结论还成立吗？写出你的猜想并加以证明；
，则Q=_________（用
答案
（1）如图，
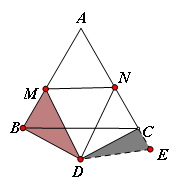
BM、NC、MN之间的数量关系BM+NC=MN．此时
．（2）猜想：结论仍然成立．
证明：如图，延长AC至E，使CE=BM，连接DE．
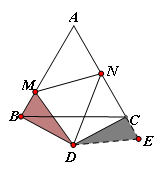
∵BD=CD，且∠BDC=120°，∴∠DBC=∠DCB=30°．
又△ABC是等边三角形，∴∠MBD=∠NCD=90°．
在△MBD与△ECD中：BM=CE、∠MBD=∠ECD、BD=DC
∴△MBD≌△ECD（SAS）．
∴DM=DE，∠BDM=∠CDE．
∴∠EDN=∠BDC-∠MDN=60°．
在△MDN与△EDN中：DM=DE、∠MDN=∠EDN、DN=DN
∴△MDN≌△EDN（SAS）．
∴MN=NE=NC+BM．
△AMN的周长Q=AM+AN+MN
=AM+AN+（NC+BM）
=（AM+BM）+（AN+NC）
=AB+AC
=2AB．
而等边△ABC的周长L=3AB．
∴
．
（3）如图，
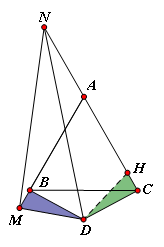
当M、N分别在AB、CA的延长线上时，若AN=x，则Q=2x+
（用x、L表示）．
知识点：全等三角形的判定与性质 旋转的性质
（1）观察特征：①大角夹半角：∠BDC=120°，∠MDN=60°；②大角等线段交于一点；
思路一：易证三角形MDN为等边三角形，可得MN=2BM=2NC
思路二：1.旋转（顺时针旋转△BMD120°，使得BD与DC重合）
2.此时可证△NDM≌△NDE
即MN=NC+CE=NC+BM
从而可得Q=AB+AC；因此Q：L=2：3．
（2）观察特征：①大角夹半角：∠BDC=120°，∠MDN=60°；②大角等线段交于一点；
解题思路：1.旋转（顺时针旋转△BMD120°，使得BD与DC重合）
2.此时可证△NDM≌△NDE
即MN=NC+CE=NC+BM
从而可得Q=AB+AC；
因此Q：L=2：3．
（3）类比（2）的解题方法：
1.旋转（顺时针旋转△BMD120°，使得BD与DC重合）
2.此时可证△NDM≌△NDH
详细分析：我们可通过构建全等三角形来实现线段的转换，思路同（2）过D作∠CDH=∠MDB，三角形BDM和CDH中，由（1）中已经得出的∠DCH=∠MBD=90°，我们做的角∠BDM=∠CDH，BD=CD因此两三角形全等（ASA）．那么BM=CH，DM=DH，三角形MDN和NDH中，已知的条件有MD=DH，一条公共边ND，要想证得两三角形全等就需要知道∠MDN=∠HDN，因为∠CDH=∠MDB，因此∠MDH=∠BDC=120°，因为∠MDN=60°，那么∠NDH=120°-60°=60°，因此∠MDN=∠NDH，这样就构成了两三角形全等的条件．三角形MDN和DNH就全等了．那么NM=NH=AN+AC-BM，三角形AMN的周长Q=AN+AM+MN=AN+AB+BM+AN+AC-BM=2AN+2AB．因为AN=x，AB=
L，因此三角形AMN的周长Q=2x+
L．
略
WORD格式（
