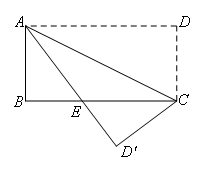
如图,把长方形ABCD沿AC折叠,AD落在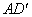 处,
处,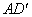 交BC于点E,已知AB=2cm,BC=4cm,则EC的长为( )
交BC于点E,已知AB=2cm,BC=4cm,则EC的长为( )
- A.2cm
- B.
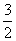 cm
cm - C.5cm
- D.
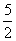 cm
cm
答案
正确答案:D
知识点:略
如图,由折叠知,∠DAC=∠EAC,
∵AD∥BC,
∴∠DAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=EC
设EC=x,则AE=EC=x
∵BC=4,
∴BE=4-x
在Rt△ABE中,∠B=90°,AB=2,BE=4-x,AE=x,
由勾股定理得,![]()
解得,![]()
即EC的长为![]() cm
cm
故选D.
略








