已知：如图，AB=AC，ME⊥AB，MF⊥AC，垂足分别是E，F，ME=MF．
求证：MB=MC．
下列证明思路正确的是( )
- A.连接AM，直接证明△ABM≌△ACM，得MB=MC
- B.过点A作AM⊥BC于点M，证明△AEM≌△AFM，再证明△BEM≌△CFM，得MB=MC
- C.连接AM，证明△AEM≌△AFM，再证明△BEM≌△CFM，得MB=MC
- D.过点A作AM⊥BC于点M，直接证明△ABM≌△ACM，得MB=MC
答案
正确答案：C
知识点：略
证明：如图，连接AM．
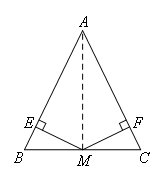
∵ME⊥AB，MF⊥AC
∴∠MEA=∠MFA=90°
∠MEB=∠MFC=90°
在Rt△AEM和Rt△AFM中
∴AE=AF（全等三角形对应边相等）
∵AB=AC
∴AB-AE=AC-AF
即BE=CF
在△BEM和△CFM中
∴MB=MC（全等三角形对应边相等）
故选C．
略
WORD格式（