已知：如图，在△ABC中，BD=CD，∠1=∠2．求证：AD是∠BAC的平分线．

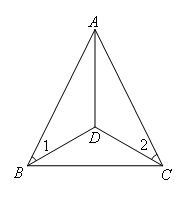
证明：如图，

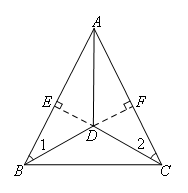
①延长CD交AB于E，延长BD交AC于F；
②过D作DE⊥AB于E，DF⊥AC于F；
；
④∴∠BED=∠CFD=∠AED=∠AFD=90°；
；
⑥；⑦．
下列证明过程正确的是( )

答案

正确答案：A

知识点：略

证明：如图，过点D作DE⊥AB于点E，DF⊥AC于点F．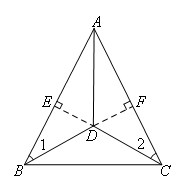

∴∠BED=∠CFD=∠AED=∠AFD=90°
在△BDE和△CDF中

∴DE=DF（全等三角形对应边相等）
∴点D在∠BAC的平分线上
即AD是∠BAC的平分线
空缺处依次所填应为②④⑥③．
故选A．

略

下载次数：0