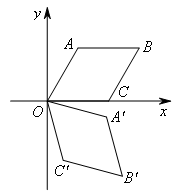
如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为( )
- A.(
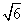 ,
,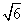 )
) - B.(2,-2)
- C.(
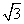 ,-3)
,-3) - D.(
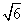 ,
,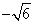 )
)
答案
正确答案:D
知识点:菱形的性质
如图,连接OB,OB′,作B′H⊥x轴于点H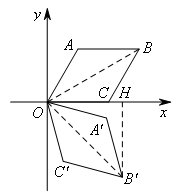
∵四边形OABC是菱形
∴OB平分∠AOC
∴∠COB=30°
又∵菱形OABC的边长为2
∴OB=![]()
∵菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′
∴∠BOB′=75°,OB′=OB=![]()
∴∠COB′=∠BOB′-∠COB=45°
∴△OB′H为等腰直角三角形
∴OH=B′H=![]()
∴点B′的坐标为(![]() ,
,![]() )
)
略








