如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E,F分别是AB,AC的中点.连接DE,DF,若四边形AEDF的周长为12,两条对角线的和等于7,则四边形AEDF的面积为( )

- A.
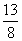
- B.
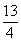
- C.
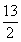
- D.10
答案
正确答案:B
知识点:略
∵AD⊥BC,点E,F分别是AB,AC的中点
∴在Rt△ADB中,DE=![]() =AE
=AE
在Rt△ADC中,DF=![]() =AF
=AF
又∵AB=AC,点E,F分别是AB,AC的中点
∴AE=AF=DE=DF
∴四边形AEDF是菱形
∵菱形AEDF的周长为12
∴AE=3
如图,连接EF,交AD于点O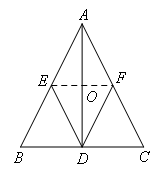
设EF=x,AD=y,则x+y=7
∴x2+2xy+y2=49①
在Rt△AOE中,EO2+AO2=AE2
∴![]()
即x2+y2=36②
联立①②可得,2xy=13
∴![]()
∴![]()
略








