如图,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为点E,且AE平分∠BAC,则AB的长为( )

- A.4
- B.
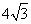
- C.
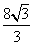
- D.
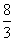
答案
正确答案:C
知识点:略
∵四边形ABCD是矩形
∴OA=OB=OC=OD,∠BAD=90°
∵AE平分∠BAC
∴∠BAE=∠OAE
∵AE⊥BD
∴∠AEB=∠AEO=90°
又AE=AE
∴△ABE≌△AOE(ASA)
∴AB=OA=OB=![]() BD
BD
设AB=x,则BD=2x
在Rt△ABD中,AD2+AB2=BD2
∵AD=8
∴82+x2=(2x)2
∴![]() ,即
,即![]()
略








