如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE.若EH=2EF,则下列结论正确的是( )

- A.AB=
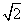 EF
EF - B.AB=2EF
- C.AB=
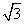 EF
EF - D.AB=
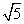 EF
EF
答案
正确答案:D
知识点:略
如图,连接AC,BD,两条线段相交于点O,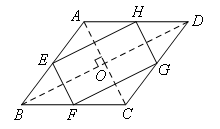
设EF=a,则EH=2a,
∵点E,H分别是边AB,DA的中点,
∴EH是△ABD的中位线,
∴BD=2EH,
∴BD=4a,
同理可得,AC=2EF,
∴AC=2a.
∵四边形ABCD是菱形,
∴AC⊥BD,![]() ,
,![]() ,
,
∴∠AOB=90°,BO=2a,AO=a,
由勾股定理可得![]() ,
,
∴![]() .
.
略








