下列说法：
①一组对边平行，另一组对边相等的四边形是平行四边形；
②顺次连接菱形的四条边的中点组成的四边形是矩形；
③四个角都相等的四边形是矩形；
④对于任意矩形ABCD，若M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合），则存在无数个四边形MNPQ是平行四边形；
正确的说法的个数是(    )

①一组对边平行且相等的四边形是平行四边形；一组对边平行，另一组对边相等的四边形，等腰梯形也满足题意，故错误；
②如图，四边形EMFN为菱形，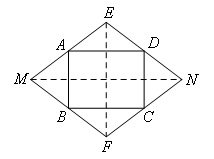

由中位线定理易得，AB∥EF∥CD，AD∥MN，，则四边形ABCD为平行四边形；由EF⊥MN，可得AB⊥AD，则可得四边形ABCD为矩形，故正确；
③四边形的内角和为360°，四个角都相等，说明四个角均为直角，则该四边形为矩形，故正确；
④如图，四边形ABCD为矩形，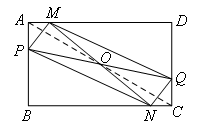

其中心为O，线段MN经过点O且满足题意，易证△AMO≌△CNO，则OM=ON，同理OP=OQ，故四边形MPNQ为平行四边形．只要满足MN，PQ相交于点O即可得到平行四边形，故存在无数个，正确
综上，②③④正确

略