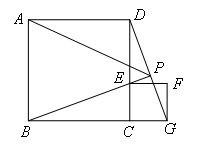
如图，正方形ABCD的边长为2，E为射线CD上一动点，以CE为边在正方形ABCD外作正方形CEFG，连接BE，DG，两直线BE，DG相交于点P，连接AP，下列说法：①△BCE≌△DCG；
②BP⊥GD；③当点E为CD的中点时，BP的长为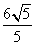．其中正确的序号是(    )

①∵四边形ABCD与四边形ECGF为正方形
∴BC=CD，∠BCE=∠DCG=90°，EC=CG
∴△BCE≌△DCG（SAS），正确；
②由①得△BCE≌△DCG
∴∠CBE=∠CDG
∴∠CBE+∠CGD=∠CDG+∠CGD=90°即∠BPG=90°
∴BP⊥GD，正确；
③连接BD
由②，BP⊥GD
∴
则由题易得，当点E为CD的中点时
BG=3，CD=2，DG=，
∴，正确．
综上，正确的为①②③．

略