如图，在等腰三角形ABC中，AB=BC，∠B=120°，M，N分别是AB，BC边上的中点．若三角形ABC的边AC上的高为1，点P是边AC上的动点，则MP+NP的和最小为(    )

作点M关于AC的对称点，连接交AC于点P，此时MP+NP的和最小．
如图所示，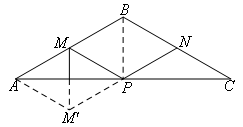

连接AM′，MP，BP．
利用轴对称的性质，并结合已知条件可得△APM′≌△CPN
（∠PAM′=∠C，AM′=CN，∠APM′=∠NPC），
因此PM′=PN，AP=PC，即P为AC中点，
利用三线合一BP⊥AC，BP平分∠ABC，故BP=1，∠CBP=60°，
再根据直角三角形斜边上的中线等于斜边的一半，得PN=BN，
所以△BNP为等边三角形，PN=BP=1，那么M′N=2PN=2．
故选B．

略